请注意,本文编写于 665 天前,最后修改于 620 天前,其中某些信息可能已经过时。
目录
本章重点
矩阵的压缩存储、广义表的操作。
第五章 数组和广义表
5.1 数组的定义和表示方法
- 数组:是由n(n>=1)个相同类型的数据元素构成的有限序列; 数组下标:每个元素的符号,数组下标从0开始;
- 存储结构:一个数组的所有元素在内存中占用一段连续的存储空间; 多维数组存储:行优先和列优先;
例
二维数组: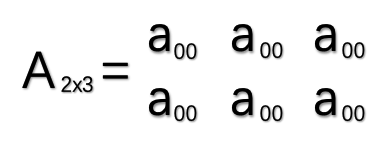
- 按行优先
| a00 | a01 | a02 | a10 | a11 | a12 |
|---|
- 按列优先
| a00 | a10 | a01 | a11 | a02 | a12 |
|---|
5.2 压缩矩阵
为矩阵中多个值相同的元素只分配一个空间,不为0元素分配空间。节省存储空间;
-
对称矩阵: = ,可以将一个n阶方阵分为上三角区、下三角区和主对角线三部分; 只存储下三角部分(含对角线),存储使用的一维数组大小为
n(n+1)/2; -
上三角矩阵:下三角区为同一常量,通常为0,存储完下三角区和主对角元素后,将常量存在最后,使用的数组大小
n(n+1)/2+1; 元素对应的数组下标
在数组内的压缩存储形式:
0 1 2(n+1)/2 a11 a12 ... a1n a22 a23 ... a2n ... C 第1行 第2行 常数项 -
下三角矩阵:上三角区为同一常量,通常为0,存储完下三角区和主对觉元素后,将常量存在最后,使用的数组大小
n(n+1)/2+1; 元素对应数组下标
在数组内的压缩存储形式:
0 1 2 3 ... ... 2(n+1)/2 a11 a21 a22 a31 ... an1 an2 ... ann C 第1行 第2行 第n行 常数项 -
稀疏矩阵:当矩阵中非零元素的个数<<j矩阵元素的个数即可视为稀疏矩阵; 零元素的分布通常没有规则,因此用非零元素的行、列和值构成一个三列的表格,可以用数组或十字链表法存储。
5.3 广义表
- 广义表:线性表的推广,一般记作 LS = (,,...,) 其中,a可以是单个元素称为LS的原子,也可以是广义表称为LS的子表;
- 表头(Head):LS非空时的第一个元素,可以是一个元素也可以是一个表;
- 表尾(Tail):LS除了表头以外的其余元素,是一个类;
例
1⃣ A = () ———— A 是一个空表,长度为0;
2⃣ B = (e) ———— B 只有一个原子e,长度为1;
3⃣ C = (a, (b, c, d)) ———— C 的长度为2,两个元素分别为原子a和子表(b, c, d);
4⃣ D = (A, B, C) ———— D 的长度为3,三个元素都是列表,D = ((), (e), (a, (b, c, d)));
5⃣ E = (a, E) ———— E 是一个递归的表,长度为2,E = (a, (a, (a, ...)));
GetHead(B) = e; GetTail(B) = (); GetHead(D) = A; GetTail(D) = (B, C);
如果对你有用的话,可以打赏哦
打赏


本文作者:Handy Zhang
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
目录